崔智元「1」、卢德维克·阿尔库里「1」、莱昂纳多·F·乌尔巴诺「2」、普尼特·马松「3」、马修·维尔米利亚「4」和摩西·卡姆「1」

计算机辅助精液分析（CASA）能够可靠分析精液图像，其设计目标是处理大量图像时保持高度一致 性、准确性和可重复性。若能获得多种条件和样本质量模式下的精液图像可靠模拟，CASA算法的设 计与测试将显著提速。

通过逼真的精液图像模拟技术，可以量化现有及新型CASA算法的性能表 现——因为模拟图像的参数既已明确又可控。我们针对实验室样本中真实二维（俯视）显微镜图像中的精子细胞图像及其运动模式，提出了模拟模型。该模型通过四种运动类型（线性移动、圆形运动、过度活跃运动和静止不动）模拟人类精子。

这些模拟模型用于研究精子细胞的分割、定位及追踪算法。在不同噪声水平下测试了多种分割与定位算法，并通过精确度、召回率及最优子模式分配（OSPA）指标进行对比分析。研究人员通过真实人类精液样本图像验证了模拟实验中获得的分割与定位观测结果。

以模拟精液图像为例，展示了不同追踪算法（最近邻算法（NN）、全局最近邻算法（GNN）、概率数据关联滤波器（PDAF）及联合概率数据关联滤波器（JPDAF）)在精子细胞追踪中的应用效果。通过多目标追踪精度（MOTP）和多目标追踪准确度（MOTA）两项指标对追踪性能进行评估。

仿真模型为精液图像处理算法的客观评估提供了有效手段。我们还演示了新型仿真工具在评估和比较分割、定位及追踪方法中的实际应用价值。

该模拟软件支持对控制模拟精液图像外观和行为的参数值进行大范围测试。用户可生成不同特性的模拟场景，并评估不同CASA算法在这些环境中的有效性。该模拟工具被用于评估和比较精液图像中精子细胞分割与追踪算法的效果。

计算机辅助精液分析（CASA）系统及其算法始终是临床医生和男科学研究者关注的焦点「1」。现代 CASA系统“旨在通过客观定量的方式测量精子结构与功能的多个维度，力求实现实验室内部及不同实验室之间的高度一致性”「12」。为达成这一目标，研究者们采用了噪声滤波、图像分割、定位、多目标追踪及机器学习等技术手段「3 – 15」。

在开发和验证CASA系统时，一个主要挑战在于如何准确评估其精液分析方法与真实标准的对比效果。要验证CASA系统，必须通过具有代表性的样本进行验证。对于实际样本而言，真实标准往往难以获取，这就促使我们使用参数可调的高质量图像模拟来验证CASA系统及其算法。这类模拟不仅能助力开发自动化精液分析系统，还能帮助不同候选算法之间进行有效比对。

为了生成精液样本视频的模拟以供评估和验证，我们需要以下内容：
(1)精子细胞图像模型（用于在模拟精液图像中生成精子细胞）。
(2)精子细胞运动模型 ，该模型定义了精液图像随时间的变化规律。

精子细胞

图1.（a）真人精液样本图像，（b）模拟精液样本图像。

本文提出的模型借鉴了针对其他细胞类型「16–21」开展的类似研究。精子细胞游动模型的开发融合了多种。

现有方法：

部分采用非线性运动方程组（Armon等22及Urbano第6章4），另一些则运用流体力学建立更精细的细胞运动描述「23–31」。

然而，现有大多数细胞动力学模拟模型「25–31」尚未整合多细胞图像——这正是CASA系统「32」、「33」等实际应用中使用的典型场景。在开发和应用相关图像模拟技术前，必须先实现单细胞描述向全尺寸多细胞图像的整合。

本文提出了精子细胞图像模型及其四种不同游动模式（圆形运动、线性运动、超活跃运动和静止状态）的模拟方法。这些模型的计算需求较低，可轻松整合到多细胞图像系统中，生成与CASA系统兼 容的多种图像格式。如图1所示，图a展示了200倍放大率的真实精液样本实拍图像，图1b则是基于左侧图像参数生成的模拟精液图像，两者并排对比直观呈现了模型效果。

方法

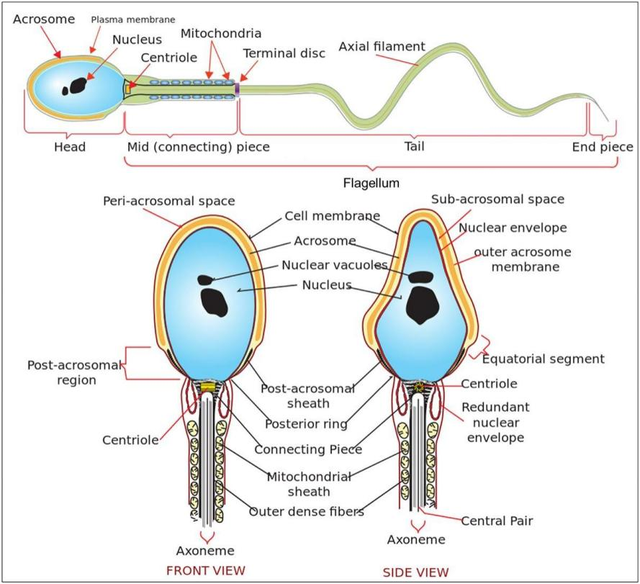图2.人类精细胞36的示意图。

图2.人类精细胞「36」的示意图。（上）精细胞的主要成分。（下）精子头部和中段的正面和侧面视图。

人类精子细胞（参见图2，引自比利亚雷亚尔（2006）36)主要由头部和鞭毛-卵黄两部分构成。鞭毛由中段、尾部（又称主体）和末端三部分组成，通过波浪式摆动推动细胞前进「37」。下文将详细解析精子头部与鞭毛的二维图像，并阐述精子运动的模型机制。

模拟精子细胞。

我们分别生成精子头部和鞭毛的图像，随后将这些元素进行整合。在构建精子细胞头部与鞭毛的模型时，我们参照了《世界卫生组织实验室 手册》 中关于人类精液检测与处理的描述「38」。人类精子头部通常呈椭圆形，其尾部（即鞭毛主体部 分）则为均匀粗细的细长圆柱体。在我们的模拟中，仅采用尾部结构来构建鞭毛模型（未考虑中间段 和末端结构，因为这些部位在CASA系统使用的分辨率下通常过于微小而难以单独观测）。

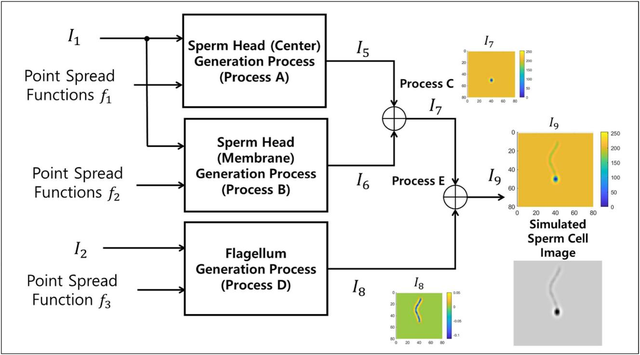图3.精子图像生成流程图

图3.精子图像生成流程图。输入包括图像I1、I2及点扩散函数1、2、3。输出I9为模拟精子图像。各步骤细节分别展示于图5、7、8、9和10。其中，图像I7显示精子头部图像（过程C输出），图像I8显示鞭毛图像（过程D输出），图像I9显示精子头部图像（过程E输出）。彩色条带标注在I 7-I9图像旁，对应显示灰度强度值。下方彩色区域展示了模拟精子细胞的灰度图像I9。

精子图像生成流程的流程图如图3所示。该流程的输入包括图像I（对应精子头部）和图像I2（对应鞭毛曲线），以及点扩散函数2、3。通过标记为过程A和B的操作分别生成精子头部中心I5和膜结构I6的图像。过程A的输入是图像I和点扩散函数，过程B的输入是图像I和点扩散函数2。在过程C中，精子头部中心I5与膜结构I6的图像被合并，生成最终的精子头部I7图像。因此，过程A-C构成了精子头部生成流程。最后，通过过程D使用图像I2和点扩散函数3生成鞭毛I8的最终图像。最终，精子头部I7与鞭毛I8的图像在过程C中被合并。

图4.模拟精子图像，其中用点表示头部的位置（绿色）和鞭毛的曲线（蓝色）。

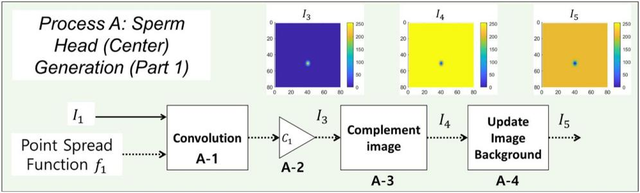图5.精子头部（中心）图像生成流程示意图

图5.精子头部（中心）图像生成流程示意图。输入为图像I1和点扩散函数1。输出为模拟生成的精子头部中心I5图像。I1与I2经卷积运算后，通过系数C1进行缩放处理生成I3（执行A-1和A-2步骤）。对图像I3进行互补运算生成I4图像（执行A-3步骤）。最后为图像I4添加背景，最终得到精子头部中心I5图像（执行A-4步骤）。

并生成精子细胞的完整图像「9」。图3中全彩模拟精子细胞图像下方显示了模拟精子细胞的灰度图像。其中，I是N个像素N的图像，

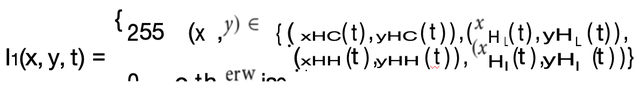公式（1）

N表示模拟图像的帧尺寸。

公式（2）

图4展示了模拟精子细胞的图像。其中绿色和蓝色分别表示精子头部位置（I1（x ，y）=255）和鞭毛轨迹（I2（x ，y）=255）的坐标点。模拟中采用0到255之间的灰度值（共256个灰度级）。

下文将详细说明五个处理流程（A-E），其流程图分别展示在图5、7、8、9和10中。需注意的是，I3-I9的图像均配有编号色阶条，可作为将彩色图像转换为灰度图像的参考依据。

流程A：精子头部（中心）生成（第一部分）。流程A的流程图如图5所示。生成精子头部的椭圆形结构（图I）通过二维正态分布滤波器A-1进行卷积处理；该滤波器作为点 (过程，二 维的扩散函数使用（参见Gonzalez「39」第3-5章）。点扩散函数的正态分布定义为

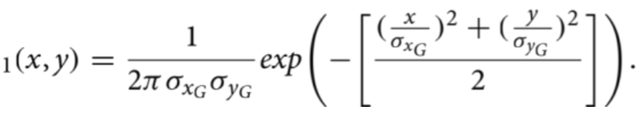公式（3）

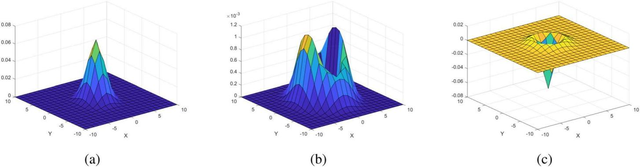图6.精子细胞图像生成过程中使用的点扩散函数；（a）1 ，（b）2 ，（c）3。

三维表面图如图6a所示。标准偏差σ xG和 σ yG分别控制细胞头部的长度与宽度。

本节示例中，σ xG=1.86像素 σyG=2.86像素。

滤波器尺寸为25×25像素(x和y范围在−12至12之间）。最终输出图像需通过恒定系数进行缩放以 设置

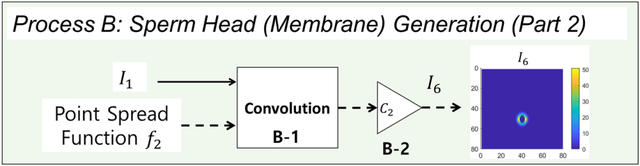图7.精子膜图像生成流程示意图

图7.精子膜图像生成流程示意图。输入为图像I1和点扩散函数2，输出为模拟精子膜图像I6。

I1与I2 进行卷积运算后，通过C1进行缩放处理，生成I6（对应B-1和B-2步骤）。

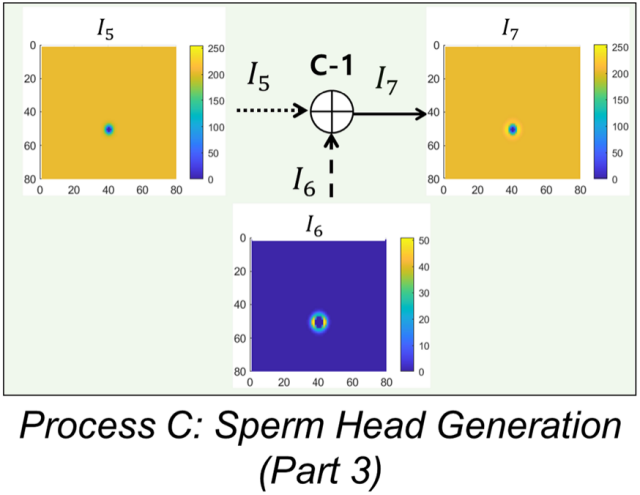图8.精子头部图像融合处理流程示意图

图8.精子头部图像融合处理流程示意图。

输入I5和I6，输出为模拟的精子头部I7。I5和I6相加生成I7（过程C-1)。

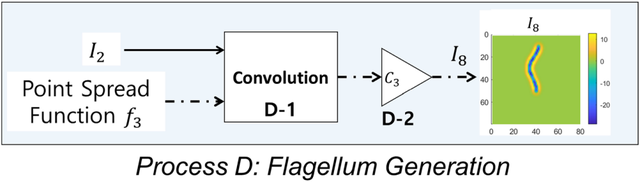图9.鞭毛生成流程图。

图9.鞭毛生成流程图。输入为图像I2和点扩散函数3。输出为鞭毛I7的模拟图像。

I2与I3经卷积运算后，通过C3进行缩放处理，最终生成I7（对应过程D-1和D-2)。

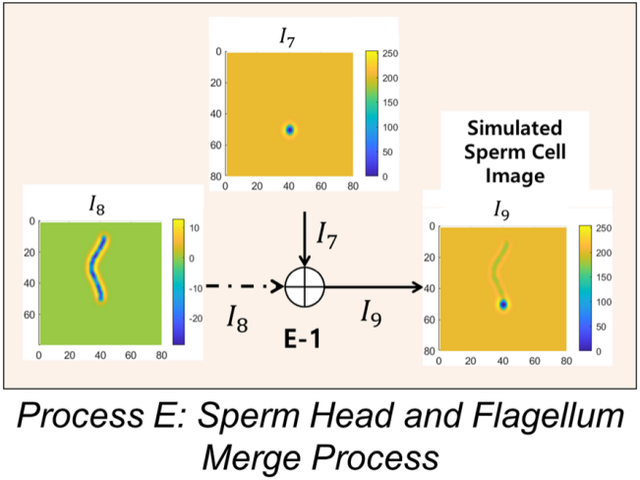图10.精子头部和鞭毛图像融合过程示意图。

图10.精子头部和鞭毛图像融合过程示意图。输入为图像I7和I8 ，输出为模拟的精子细胞I9 。

I7和I8相加生成I9（过程E-1)。

峰值强度值设定为255，记作I3（图5中的过程A-2）。通过调整常数控制细胞头部的强度值。对图像I3进行补码处理，生成白色背景上带有暗椭圆形中心的图像（过程A-3)。在过程A-4中，需添加模拟图像的背景层。设BL为将添加到模拟图像的背景层，其尺寸为N×N。

本节示例中假设背景均匀，每个像素值均为204（即BL（x ，y）=204，相当于255的80%）。从图像I4中减去255−BL的值，将所有负数置零。

最终生成的图像记作I5 (I5=max[0 ，I 4 −(255−B L]））。

流程B：精子头部（膜）生成（第二部分）。流程B的流程图如图7所示。

在典型情况下通过观察精子图像样本可以发现，其头部周围存在类似光环的膜状结构（如图1左图所示，Urbano等人「3」将其称为“马蹄形光环”）。为在图像I中生成这种环绕细胞的光环状结构，我们采用了改进版的二维正态分布拉普拉斯滤波器作为第二个点扩散函数。该二维正态分布拉普拉斯滤波器的定义为

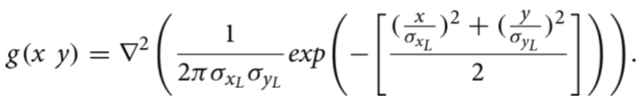公式（4）

点扩散函数2定义为 2(x, y) = max(0, g(x, y)).

点扩散函数2的生成结果如图6b所示。标准差σ x_L和 σ y_L分别控制着细胞膜的长度与宽度。本节示例中，σ x_L=2.79像素，y_L=4.29像素。滤波器2的尺寸为25×25像素（x和y范围在−12至12之间）。将2号点扩散函数与图像I进行卷积运算后，生成膜结构图像（过程B-1）。

随后对输出图像进行2倍的恒定缩放处理（过程B-2)，将峰值强度调整为51（即膜结构的峰值强度值，相当于255灰度级的20%）。该膜结构图像标记为I6。通过调节2的数值可控制膜结构的亮度参数。

过程C：精子头部形成（第三部分）。

过程C的流程图如图8所示。在过程C中，将精子头部中心I5的图像和鞭毛I6的图像叠加，得到完整的精子头部图像，如图8所示，并标记为I7。

D过程：精子鞭毛生成。图9展示了D过程的流程图。为了生成鞭毛，将图像2（公式2)与点扩散函数3（公式6)进行卷积运算，生成鞭毛具有均匀口径特征的图像。该点扩散函数3定义为高斯拉普拉斯滤波器（即当xL=yL=σf时，公式等式（4）的高斯分布）。

3D表面图如图6c所示。标准差σ控制鞭毛的宽度，在本节示例中σ=1.5像素。3号滤波器的尺寸为25×25像素（x和y范围为-12至12）。

通过恒定缩放系数3，将膜结构的峰值强度设定为13（约255像素值的5%）。通过调整3可控制鞭毛的强度。最终得到的鞭毛图像呈现为一条细长的膜状曲线，其缩放后的 图像标记为I8。

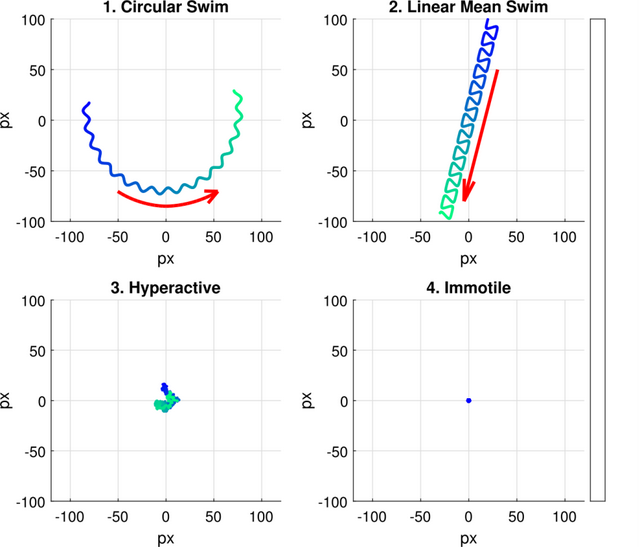图11. 四种游动模式的模拟游动轨迹

图11. 四种游动模式的模拟游动轨迹：环形游动、直线平均游动、超活跃游动和静止游动。色条 表示轨迹随时间变化的颜色，运动持续时间为4s。

过程E：精子头部与鞭毛融合。最后，在过程E中，细胞头部的图像、I7以及鞭毛（I8）被添加以形成精子细胞的图像（I9，见图3和10）。过程E如图10所示。

游泳模型。在本节中，我们将描述头部和鞭毛的游泳/运动模型。

关于精子细胞的运动模型。这些模型描述了头部和鞭毛的位置如何随时间变化。这些位置定义了用于生成I（细胞头部，等式1）和II（细胞鞭毛，等式2)的坐标点。

我们将精子运动分为以下四种游动模式：
1. 环形游泳，
2. 线性平均游动，
3. Hyperactivated
4. 不动，或死亡。

图11显示四种游动模式的模拟轨迹（每种模式持续4秒）。轨迹标示了细胞头部的位置，箭头指示运动方向。

圆形游动细胞和线性平均游动细胞会主动向前推进，无论是沿大圆形路径还是线性路径。图11上 方展示了(1)圆形游动和(2)线性平均游动的示例，红色箭头指示细胞运动方向。(3)超活化精子细胞不 会显著偏离初始位置，其运动被描述为“剧烈振荡型”、“鞭打型”或“疯狂型”「40、41」。图11左下角展示了此类细胞的典型示例。(4)不动运动型定义了几乎完全静止的细胞（如图11右下角所示）。

我们基于文献中记录的「3、8、29、33、42」等研究中的精子运动轨迹，构建了描述圆形与线性平均运动的数学模型。对于被形象描述为“疯狂”且“充满活力” 的过度活跃游动现象，我们采用布朗运动进行建模以反映细胞运动的随机性特征「43」。在后续章节中，我们将对每种运动模式进行详细阐述。

环形游动模型。一个表现出环形游动的精子细胞沿着环形路径进行振荡运动。

这种由鞭毛「33」摆动引起的运动路径可表示为正弦调制的圆形轨迹（图12)。表1给出了模拟环形游动细胞头部与鞭毛运动的方程组。细胞头部的二维位置由方程（7a）和（7b）确定。r_c表示整体圆形轨迹的半径，s为圆形轨迹上的正弦调制频率（Hz），a是圆形轨迹上的正弦调制振幅，c为圆形周期频率（每秒周期数）。C xc和ycb分别表示水平和垂直方向的偏移量。

表1. 圆形游动细胞的模拟结果

表1. 圆形游动细胞的模拟结果。（x H y H）：圆形游动细胞头部位置。

r c：圆周路径的半径。
a：沿圆周路径正弦调制的振幅。
s：频率。

在环形路径上进行正弦调制的频率（Hz）。

c：环形周期的频率（周期/秒）。
（C xc Cyc）：垂直方向以及水平偏移常数。
（x TailC y TailC ）：沿鞭毛中心的一组k个点，位于环形结构的鞭毛上。

游泳细胞。
λ ：鞭毛的波长（即鞭毛起始点与末端之间的距离）。
R (·) ：旋转矩阵。
b (·) : 鞭毛沿其长度方向的局部振幅变化。

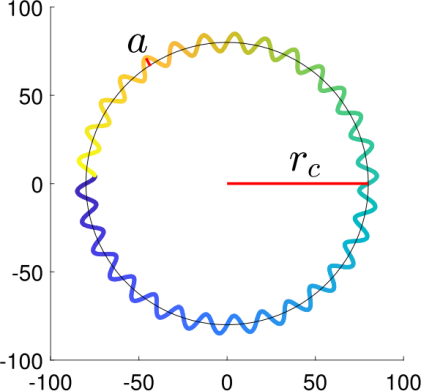
图12.模拟的圆形游动细胞的运动轨迹

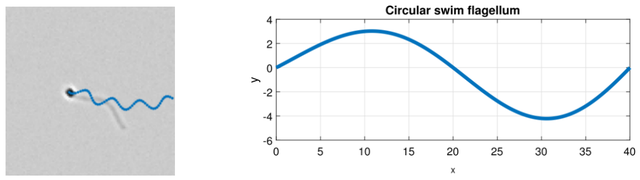图13.

图13.（左）圆形游动细胞模拟图像，蓝色显示过去轨迹。（右）圆形游动细胞鞭毛的示意图。在本例中，波长(λ)为40像素，振幅（a）为4像素。

T_c（kt）y T_c(k)）是鞭毛中心曲线上各点的笛卡尔坐标，其中k= 1,2,3 ，... ，M（默认设置中 M=200）。圆形游动细胞的鞭毛遵循德雷斯纳提出的精子鞭毛模型（公式8a)24。公式8a决定了鞭毛的振荡幅度（x T_c ），而公式8b则确定了鞭毛的端到端长度（波长 λ , 即鞭毛起始点与末端之间的距 离）。b（k）表示沿鞭毛分布的局部振幅变化。xT_c yT_c)通过旋转矩阵R (·) 调整运动方向后，被平移至精子头部位置（x HC y HC）（公式9）。圆形游动细胞的鞭毛数据点标记为x 尾部C ytailC 。本文示例中，振幅局部变化量b（k）遵循仿射函数

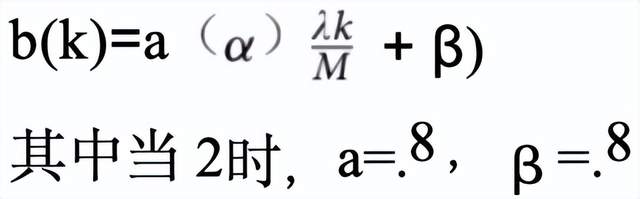针对圆形游动细胞

此处，a表示沿圆形路径振动的正弦波振幅，而λ为鞭毛的波长。图13展示了一个环形游动细胞的模拟鞭毛示例。左侧是环形游动细胞的模拟图像，蓝色线条显示 了其运动轨迹。右侧是一条曲线，代表该细胞的鞭毛。此示例中，振幅a为4像素，波长λ为40像素。

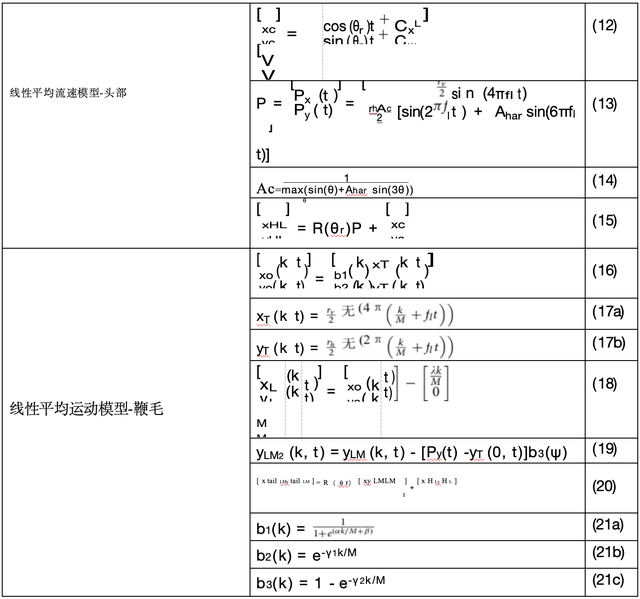表2.线性平均游动细胞的模拟结果

表2.线性平均游动细胞的模拟结果。

（x H y H）：精子头部在直线运动中的位置。

游动细胞参数设置：
（C x_L CyL）：水平与垂直方向偏移量（像素）。
V：直线路径移动速度（像素/秒）。
fl：带状区 域角度变化率（赫兹）。
r h r v：带状区域宽度与高度（像素）。
Ahar：用户自定义的第一谐波与第三谐波比例系数。
A c：针对设定宽度的校正常数。

带状结构。

θ r：正向运动方向（弧度）。
(x 尾部LMy尾部LM）：沿中心线分布的k个点集合。
线性平均游动细胞鞭毛的参数。
b 1 (k) 、b 2 (k)：鞭毛摆动时局部水平和垂直方向的变化量鞭毛上的振幅。
b 3 (k)：鞭毛位置校正函数。

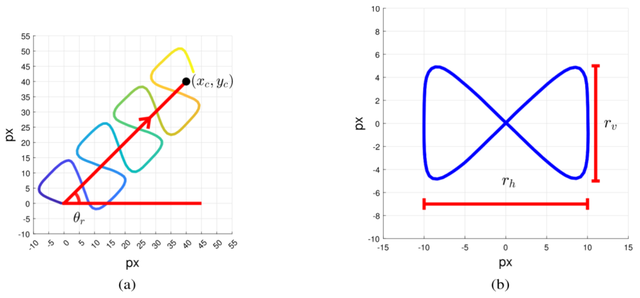图14

图14.（a）模拟线性平均游动细胞的运动轨迹（公式12-15)；（b）线性平均游动细胞沿直线路径 的带状振荡运动（公式13)

线性平均游动模型。在该模型中，精子细胞沿直线路径移动，同时进行侧向滚动。

当其向前推进时，这一特征会导致围绕直线的带状运动。用于模拟线性均速游动细胞头部和鞭毛运动的方程列于表2中。

我们使用公式（12-15）生成细胞头部的运动轨迹（沿直线路径的带状运动）。其中，沿直线路径的位置用（x c y c）表示，而沿带状运动的位置则用（P x (t) P y(t)）表示。最终的运动轨迹如图14a所示。

直线路径是时间t 的线性函数，其初始位置为（C x_L Cy_L ）。该直线路径是从初始位置（C x_L Cy_L ）到点（x c y c）的一段线性区段（如图14所示）。沿此直线路径的水平坐标（x c y c）和垂直坐标随时间变化的速率分别对应水平方向 与垂直方向的速度。

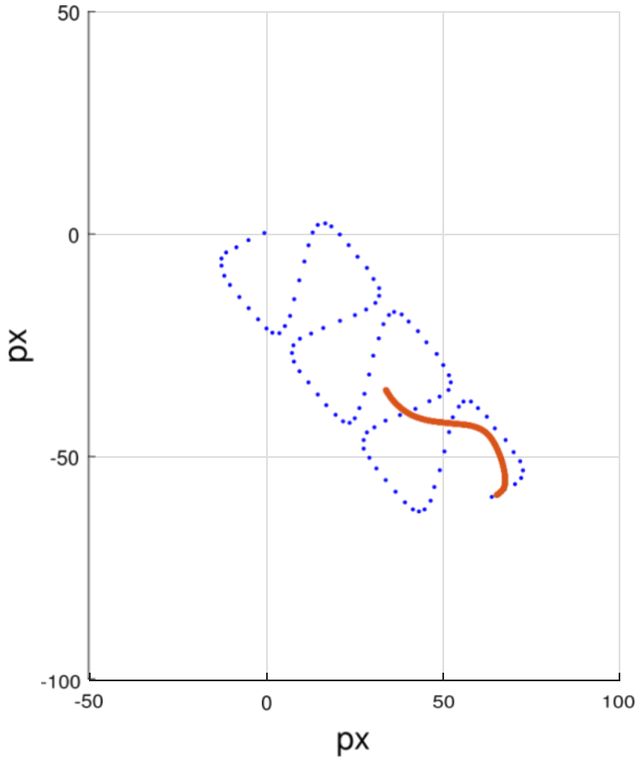图15

图15.线性平均游动细胞精子鞭毛生成示例。（橙色）模拟鞭毛。（蓝色）线性平均游动细胞 轨迹。

沿正向运动的位移量 θ r（公式12) 。沿“带状”路径（P x (t) P y (t)）的位置由公式（13-14）生成。该带 状结构如图14b所示，其中r v表示带高，r h为宽度。P x(t)和P y (t)是t 的周期性函数。Px(t)是一个频率为2f

所得的带状路径如图14b所示。Ahar是函数P y (t)中两 个正弦波的比值。

本文中的示例采用A har=0.1。

细胞在带状路径上的位置（P x(t)y(t)）乘以旋转矩阵R (·) , 得到绕轴θr的旋转变换（式15 ，R ( θr）P）。最后，将带状路径上的位置R ( θr）P与直线路径（xc ，yc)上的位置相加，即可定 义精子头部在任意时刻的精确位置（式15)。

鞭毛的生成通过方程（16-21）实现。我们采用德累斯顿模型来定义鞭毛中的水平和垂直振荡（x o （k t）yo（k t））。其中x □（k t）和y □（k t）是时间t时k =1,2,3 ，... ，M处的离散坐标点。本模拟中 M 的取值为200 。图15展示了线性平均游动细胞的鞭毛模拟示例，蓝色圆点表示精子头部的连续位置，其中部分位置对应的橙色鞭毛轨迹也一并展示。我们通过分析带状结构在水平方向（P x(t)l 的基 频2f）和垂直方向（P y(t)l 的基频f）的振动频率，利用方程（13）和（17）确定鞭毛运动模式。具体 而言，x T（k t）和y T（k t）的局部振幅变化分别对应b(ψ)和2b(k)（方程（21a）和（21b）)。

函数b(k)（公式21a）是一个转换后的S型曲线，其中α和β的值决定了函数的移位和压缩/扩展；

b 2 (k)（公式21b)是一个衰减指数函数。这两个函数共同提供了理想的实际视觉效果。

我们定义从鞭毛头部到末端的一条线段将振荡信号x □ (k t）和y □（k t ）叠加到这条直线（方程18）上。

由于我们仅考虑了P y(t)的基本频率分量f1来生成（y T（k t）），因此头部位置的垂直坐标P y(t)与 鞭毛位置的垂直坐标yT（kt）之间的差异会导致鞭毛定位偏移。这种偏差可通过公式（19）和 （21c）进行校正。

最后，鞭毛会旋转以匹配运动方向，并移动到细胞头部的位置（公式20) 。在本文提供的示例中， 公式（21a）、（21b）和（21c）中的常数设定为：α=22 ，β=-2 ，γ 1=5 ，γ 2= 1.5。

超活跃游泳模型。用于模拟超活体头部和鞭毛运动的方程式。

活跃的游动细胞数据详见表3 。在x和y两个维度上，每个细胞的运动轨迹均遵循等式方程。

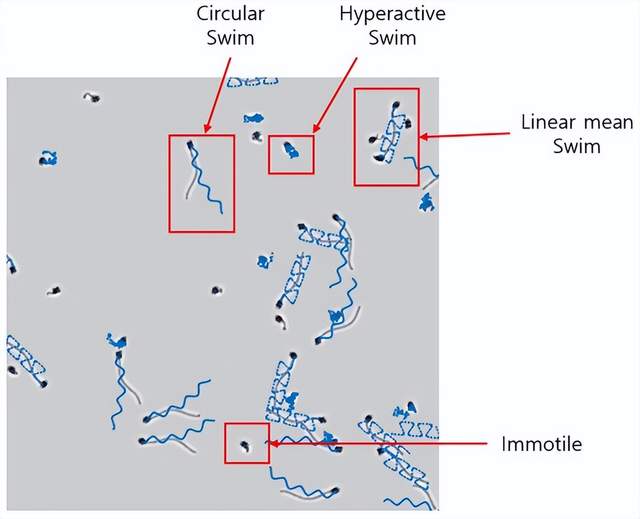图16.模拟图像示例，其中每个细胞的轨迹用蓝色表示。

静止或死亡细胞模型。将静止或死亡细胞模拟为非移动对象，并使用以下方程式：

不动细胞的头部和鞭毛运动的模型如表4所示。

在整个模拟过程中，细胞的头部和鞭毛将保持静止（方程25、26) 。鞭毛的生成是通过截取高活性细胞的鞭毛快照实现的。而不动细胞的鞭毛则使用等式（26）进行生成。

图16展示了模拟精液样本的示例，其中可以观察到四种不同游动模式的精子细胞。每个细胞的运动轨迹均以蓝色线条呈现。在Choi等人开发的模拟软件（参见文献「34」)中，用户可通过调整细胞浓度、形态特征和游动模式等参数，生成符合需求的精液图像用于测试。

在图17中，我们展示了另外3个模拟特征场景。这些模拟特征用于生成动态场景，以测试CASA算法和系统。

第一个功能为每个精子细胞的位置添加噪声（示例如图17a所示）。添加噪声用于模拟由细胞和周 围流体引起的随机运动。

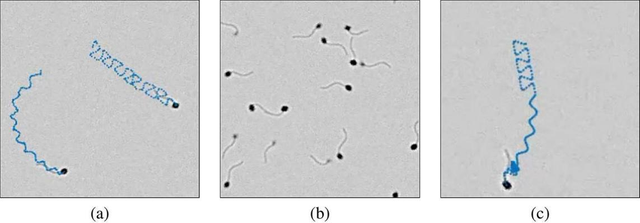图17

图17.（a）两个细胞的模拟图像，带有加性随机噪声，两个细胞的轨迹用蓝色表示。本例中的随机噪声是高斯随机变量。(b)精子细胞的模拟图像，具有可变强度。(c)精子细胞的模拟图像，向其他游动模式转变。

表5.分割和定位测试的模拟参数

第二个功能模块为每个精子细胞分配不同亮度值（示例见图17b）。该功能旨在模拟因观察精液样本所用腔室或载玻片深度不同而导致精子细胞呈现差异的环境。常规精液观察腔深10至20微米「38」。部分细胞可能游动在腔体深处，而其他细胞则靠近顶部游动，这会导致部分细胞呈现颜色暗淡现象。第二个功能模块正是为了模拟这种场景而设计。

精子细胞的游动模式会随着时间推移不断变化「32」。第三个特征是通过设定转移概率来定义细胞从一种游动模式转换为另一种模式的可能性。如图17c所示案例，一个精子细胞会依次经历线性游动、圆周游动和超活跃游动阶段。举个具体例子：假设处于线性游动状态的细胞在1秒后有85%的概率保持当前状态，10%的概率转变为圆周游动，5%的概率转变为超活跃游动（完全停止游动的概率为0%）。我们在Choi等人的研究「34」中，提供了基于这三种不同功能生成的示例图像作为说明。